Thermal Design Basics | Practical Example

One of my portable police scanners has an external 6V jack. To use it in my car I used my standard linear voltage regulator board and a high quality ST L7806 voltage regulator to get the ~13.8V of the car down to 6V. Maximum observed current of the scanner was 0.25A. So the thermal design question of the day is: How hot will the linear regulator get and do I need a heatsink?

Universal Linear Regulator Board

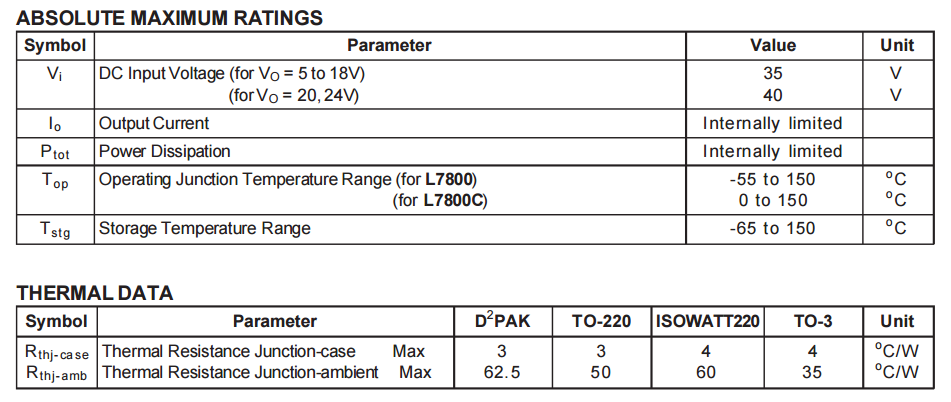
So lets start with the obvious first question: How hot is too hot? The answer is of course to be found in the datasheet. The datasheet states an absolute maximum of 150 °C. Note that this is the maximum rating though. While you can safely run the device at 150 °C, you probably don’t want to. Remember that 100 °C is the boiling point of water. So 150 °C is pretty darn hot. But it’s within the parameters given to us.

ST L7800 Datasheet

So how do we calculate how hot the device gets? The key to that question is the dissipated power and a figure called the thermal resistance junction-ambient, symbolized as theta-ja (θ_ja). It is also shown in the previous datasheet snapshot. This figure basically says how many degrees the device’s junction temperature rises ABOVE ambient temperature for a given amount of dissipated power. Ambient temperature, or “room temperature” is often assumed to be at 25 °C. And that’s what we’re gonna work with but when you do the math, please be practical. If you can reasonably expect the temperature to rise above 25 °C, then do the math accordingly.

So our formula for junction temperature is this:

T_junction = T_ambient + (θ_ja * power)

Alright, let’s piece together what we have. Let’s start with the dissipated power. We put in 13.8 V at 0.25 A and get out 6V. That makes 1.95 Watts ([13.8V – 6V] * 0.25A) of power to turn into heat. To calculate the expected junction temperature we simply plug all the values into the formula and solve.

25 + (50 * 1.95) = 122.5 °C

That means we can expect the junction temperature of the device to reach 122.5 °C. This is within the given maximum ratings and thus the answer to the heatsink question is no, we do not need a heatsink.

But not the reality check, think along with me. Again remember that 100 °C is the boiling point of water. Do we really want a device 22.5 °C above that sitting around somewhere? And also we assumed ambient to be at 25 °C. Car ambient temperatures frequently rise well above that, especially when exposed to sunlight. On top of that, car voltages aren’t even close to stable and can exceed 14 volts easily. So the practical answer would be that we would elect to use a heatsink. And that’s exactly what I did.

How to size heatsinks is a more complicated story and will be part of a different article.

Links and Sources:

[1] L7800 Series Datasheet, ST: https://baltic-lab.com/wp-content/uploads/2016/01/L7800.pdf