Total Harmonic Distortion (THD) from dBc

How to calculate THD from dBc

This article supplements to my article titled THD Measurement with an Oscilloscope and FFT, which appeared in Elektormagazine [1]. Here I will explain how the formula to calculate THD-F from relative power values (in dBc) was derrived from the standard voltage-ratio formula. A more in-depth explanation of the entire subject can be found in my research paper titled Total Harmonic Distortion (THD) analysis utilizing the FFT capabilities of modern digital storage oscilloscopes [2].

The basic equation for calculating THD-F is as follows:

$THD_F &= \frac {\sqrt {\sum_{n=2}^{\infty} V_n^2}} {V_1}$

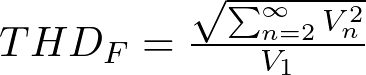
V1 refers to the rms voltage amplitude of the fundamental frequency (also called 1st harmonic), Vn refers to the rms voltage amplitudes of the n-order harmonics of the fundamental frequency.

This formula can be written in its expanded. A poperty that will become useful later. The expanded form is as follows:

$THD_F &= \sqrt{\frac {V_2^2} {V_1^2} + \frac {V_3^2} {V_1^2} + \frac {V_4^2} {V_1^2} + \frac {V_5^2} {V_1^2}} ...$

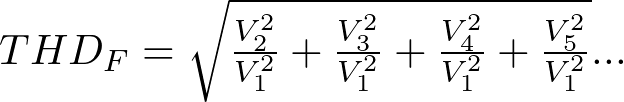
The equation for relative power measurements in dBc is as follows:

$dBc &= 10\log_{10}(\frac {P_n}{P_1})$

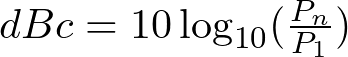
Where Pn is the power of the n-order harmonic in dBm, P1 is the power of the reference carrier, in this use case the power of the fundamental frequency.

The fact that Power is defined as rms Voltage squared and the system impedance will be equal for both Pn and P1, the Pn to P1 power ratio is equal to the ratio of the squared rms voltage amplitudes of the corresponding signals:

$\frac {P_n}{P_c} = \frac{\frac{V_n^2}{R}}{\frac{V_1^2}{R}} = \frac {V_n^2}{V_1^2}$

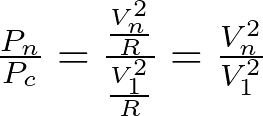
Looking back at the second formula, it becomes obvious why this property is useful. This property can now be combined with the (expanded) THD-F formula, yielding the following, compact equation:

$THD_F &= \sqrt {\sum_{n=2}^{\infty} 10^{(P_n/10)}}$

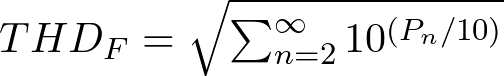
Links and Sources:

[1] Westerhold, S. (2023), THD Measurement with an Oscilloscope and FFT: https://www.elektormagazine.com/magazine/elektor-288/61444
[2] Westerhold, S. (2022). Total Harmonic Distortion (THD) analysis utilizing the FFT capabilities of modern digital storage oscilloscopes. https://www.researchgate.net/publication/362542224

Please cite this article as:
Westerhold, S. (2023), "Total Harmonic Distortion (THD) from dBc". Baltic Lab High Frequency Projects Blog. ISSN (Online): 2751-8140., https://baltic-lab.com/2023/01/thd/, (accessed: November 23, 2024).

Funding:

If you liked this content, please consider contributing. Any help is greatly appreciated.

How to calculate THD from dBc

Leave a comment Cancel reply