L-Network impedance matching

Posted on by 27 Comments
Impedance matching is an everyday problem for RF circuit designers. The L-Network is one of the easiest lossless ways of matching a low source impedance to a higher load impedance. This article shows how they work and how to design them.

Matching a transistor amplifier’s low output impedance with the higher impedance of an antenna (typically 50 or 75 Ohms) is just one everyday example of where an L-Network can be used. For this article, we are going to design an L-Network that matches a 75 Ohm source (function generator) with a 1 kΩ load (resistor).

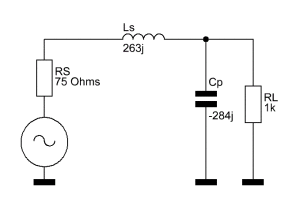
To make it easier for you to understand how this network works, I will present the complete circuit first, explain how it works and then explain how the values are being calculated. Here is the finished L-Network:

L-Network matching 75 Ohms source impedance to 1000 Ohms load impedance

L-Network matching 75 Ohms source impedance to 1000 Ohms load impedance

RS = Source Resistance (75 Ohms)
RL = Load Resistance
Ls = Series inductance (j263)
Cp = Parallel Capacitance (-j284)

Don’t be frightened by the little “j” in front of the values, in case you have never seen it. The letter “j” in electronics engineering stands for the imaginary unit. Adding “j” to a reactance is basically the so-called “vector notation.” A positive value indicates an inductive reactance and a negative value is always a capacitive reactance. If you are not used to it, you can just think of Ls as an inductor with a reactance of 263 Ohms and of Cp as a capacitor with a reactance of 284 Ohms.

Note that the reactance of a capacitor and an inductor is frequency dependent. Therefore, this circuit does not work well over a large bandwidth.

This circuit makes the 1000 Ohms load ‘look’ like a 75 Ohms load to the source. But how does it work? To answer this question, we have to look at the equivalent circuit. For that, we will reduce the overall circuit to simpler elements, step by step.

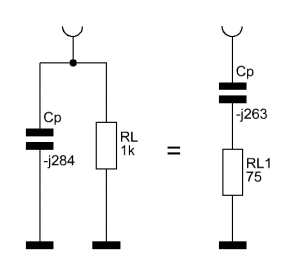
Let’s start with Cp and RL. They are in parallel. The overall impedance of two resistors is calculated as follows:

R = \frac{R_1 * R_2}{R_1 + R_2}&

Likewise, the resulting complex impedance of a resistor and a capacitor can be calculated as follows:

Z = \frac{Xc * R}{Xc + R}&

In our case, we get:

Z = \frac{X_c * R_L}{Xc + R_L} = \frac{-j284 * 1000}{-j284 + 1000} = 75-j263&

75 is the real part in Ohms and -j263 is a capacitive reactance of 263 Ohms. That means the capacitor and resistor in parallel will act like a resistor with 75 Ohms and a capacitor with 263 Ohms reactance in series.

Equivalent circuit for Cp and RL

Equivalent circuit for Cp and RL

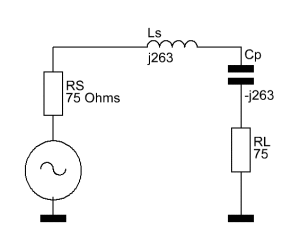
Now if you insert that back into the original circuit and have a close look at it, you may notice something. Look at the reactance of Cp and Ls.

Overall equivalent circuit after reducing Cp and RL to a series equivalent circuit

Overall equivalent circuit after reducing Cp and RL to a series equivalent circuit

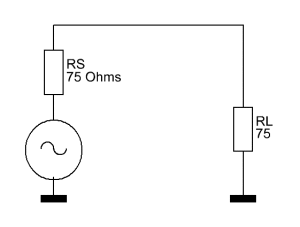
Correct, the reactance of both the capacitor and the inductor are the same, just with different vectors. If you have never worked with a complex impedance beforehand, you will now be amazed by how much easier it makes things. We can simply add the reactances together, and since 263 + -263 is zero, we only have the 75 Ohms load resistance left. Yes, it’s that simple, the source ‘sees’ the 1 kΩ load as a 75 Ω load.

Overall equivalent circuit of the L-Network

Overall equivalent circuit of the L-Network

An often-welcomed side effect is that this L-Network acts as a low-pass filter. So, if it’s used to match a low transistor amplifier impedance directly to the higher antenna impedance, one suppresses harmonics at the same time.

If one wishes to have a high-pass characteristic, one can simply switch the positions of the inductor and the capacitor. It really changes nothing. The impedance values, of course, need to be properly adjusted in that case.

Let’s talk about how to design a circuit like this from scratch. We will use the above values, source impedance of 75 Ohms and load impedance of 1000 Ohms at a frequency of 16 MHz. The frequency doesn’t matter until the end when we have to pick actual values for Ls and Cp.

The first thing we have to calculate is the quality factor, or Q factor. It describes how under-damped an oscillator or resonator is, or equivalently, characterizes a resonator’s bandwidth relative to its center frequency. The Q of an L-Network is calculated as follow:

Q = \sqrt{\frac{R_{Load}}{R_{Source}}-1}&

RLoad = Load Resistance
RSource = Source Resistance

With our values plugged into the equation, we get the following:

Q = \sqrt{\frac{1000}{75}-1} = 3.512&

So 3.512 is our Q. The rest is just as simple. To get the needed impedance of the inductor, we use the following formula:

X_L = Q*R_{Source} = 3.512 * 75 = 263&

That means the inductor needs to have an impedance of 263 Ohms at the desired frequency. We can write this as j263 to make sure it’s apparent that it is an inductive reactance. The impedance of the capacitor needs to be the load resistance divided by the Q factor.

X_C = \frac{R_{Load}}{Q} = \frac{1000}{3.512} = 284&

Again, this means that the impedance of the capacitor at the desired frequency needs to be 284 Ohms. Using the vector notation, we write -j284 to indicate that it is a capacitive impedance.

Okay, now we need to find actual values for the inductor and the capacitor. To be able to calculate either one, we need to settle on an operating frequency. For this article we will use 16 MHz. Using the following formulas, we can find the actual values for the parts at the desired frequency:

L = \frac{X_L}{\omega} = \frac{263}{2 \pi (16*10^6)} = 2.6 \mu H&

That means our inductor needs to have a value of 2.6 μH. I chose a value of 2.2 μH as it is a common value I had in stock. Since the circuitry itself in real life usually contains what’s called parasitic inductance, it won’t throw the circuit off by far. Next up is the capacitor:

C = \frac{1}{\omega X_C} = \frac{1}{2 \pi (16*10^6) 284} = 35 pF&

Instead of 35 pF, I used a 33 pF capacitor. Not only is it a more common value, we can again assume a little bit of stray capacitance by the remaining circuit.

75 Ohms to 1000 Ohms L-Network characterized with a return loss bridge

75 Ohms to 1000 Ohms L-Network characterized with a return loss bridge

I used a return loss bridge, a signal generator and an oscilloscope to verify the performance of this circuit. And sure enough, it acts just like a 75 Ohm resistive terminator at about 16 MHz. The exact frequency for best operation turned out to be roughly 16.1 MHz.

Confirming the performance of the 75 Ohms to 1000 Ohms L-Network using the Teledyne LeCroy HDO4024

Confirming the performance of the 75 Ohms to 1000 Ohms L-Network using the Teledyne LeCroy HDO4024

Update (04/06/2013): I previously wrote that one can not match a high impedance source to a low impedance load. That is incorrect. Naturally, it works perfectly fine the other way around. One only has to switch the position of the load and the source.

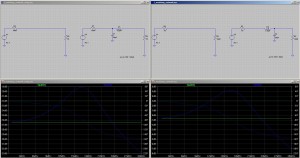
KJ6QBA took out the time to simulate this circuit using LTspice. He also simulated the same circuit used in reverse to match a 1000 Ohm source to a 75 Ohm load. Here’s the result:

LTspice simulation of the L-Network provided by KJ6QBA

LTspice simulation of the L-Network provided by KJ6QBA

Please cite this article as:
Westerhold, S. (2013), "L-Network impedance matching". Baltic Lab High Frequency Projects Blog. ISSN (Online): 2751-8140., https://baltic-lab.com/2013/04/l-network-impedance-matching/, (accessed: November 21, 2024).

Funding:

If you liked this content, please consider contributing. Any help is greatly appreciated.

27 thoughts on “L-Network impedance matching”

  1. Would have been nicer without the lecroy ad in the last image, but that’s very cool anyways. The description is very clear, thanks, I learnt something today.

    • No ad in there. The reason I mention the scope the way I do is SEO. Other than that, I think it’s a great scope and it deserves to be mentioned.

  2. “The only problem with this circuit is that it only matches a low source impedance to a higher impedance.”

    The key is the element closest to the load. If it is a shunt element, it can reduce the load impedance `seen` at the source. If it is a series element, it `increases` the load impedance `seen`.

    • Yes, that’s correct. I should change the article to clarify that this particular configuration only works as ‘step-up’ impedance converter. Then again, I might as well explain that the same in ‘reverse’ works as ‘step-down’. In either case, thanks for the comment. I got tempted into writing it the way I did without thinking as one rarely sees L-Networks as step down, mostly pi-Networks are used. Good catch, thanks!

      • Nicely done. So how about now do the step up version with a Pi network, and show how it looks on the Smith chart? That would be very instructive.

        • Working on that. Before I start posting smith charts on my blog I’ll actually write an article on how to read a smith chart. My intend is to not post challenging information that isn’t explained anywhere else in my blog.

          • Your website is wonderful, thanks for this post in particular. I, too, am a fan of clearly written explanations. So in that spirit, can you explain where the Q factor of the L-network came from? Why is it equal to the square root of ([the ratio of the load resistance to the source resistance] – 1)? Thanks and looking forward to more great stuff from you!

  3. Would you mind breaking down the algebra on:

    ((-j284*1000)/(-j284+1000))?

    It’s been many years for me
    Thanks either way,
    Steve

  4. Pingback: KF5OBS #3: L-Network Impedance Matching: | KF5OBS /IP

  6. I am clear with this 🙂 thank you 🙂 it would be nice if you could help us with T and pi network 🙂

  9. This could very nicely be followed by an RF amplifier with impedance matching characteristics…Would love to see a complete tutorial on RF amplifier design, since the youtube seems to be lacking any clear explanations. Great tutorial by the way. I’m doing an RF amplifier design for 150 MHz and I was trying to scale the 7 MHz design I saw in ‘Experimental Methods in RF design’. This gave me an excellent foundation to build from. Keep going! Thanks…

  12. I was able to get the math to work after watching some tutorials on YouTube. Search for imaginary number math basics 101

  14. Hello KF5OBS: I loved your tutorial and video. However I am a little confused on the math. The eq. is Xc*R which my calcultator say is (284*1000 = 284000) then divided by (284 + 1000 = 1284). This would then give me (284000/1284 =221.8). Not 263 which you came up with.

    The in the next step you say: (Correct, the reactance of both the capacitor and the inductor are the same ) , which to me is actually would come out Ls=263 and Cp=221. I am confused what am I looking at wrong. Thank you for your help. Would very much like to know what I did wrong. Thanks Ken AC2QZ.

  15. In the simulation by KJ6QBA, shouldn’t the gain for the blue curves at 16.1MHz be the same for both plots? If Rs and RL are equal in both simulation cases, shouldn’t it simply cut the voltage in half? In the first simulation it is at -19dB and the second one is 5dB.

  16. Is it possible to do a L matching network with a High-Pass filter?. This one calculation is used in RF antennas matching network?.

    Regards.

  17. Will you please calculate the L & C values for Rsource= 200Ohm and Rload= 50Ohm. I am finding it out difficult, please answer it

Leave a comment

Your email address will not be published. Required fields are marked *