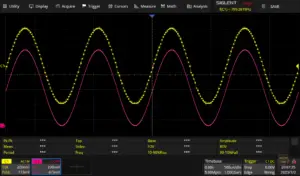
DSP Diode Clipping Algorithm for Overdrive and Distortion Effects
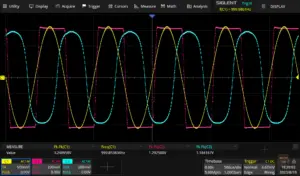
This article shows how to approximate the behaviour of a regular diode in a mathematical equation and how to subsequently implement the behaviour in software. The DSP algorithm can be modified to implement different topologies, such as single diode clipping, dual diode symmetrical soft clipping or asymmetrical clipping.